|
Aircraft
and Human Performance |
Aircraft Systems
|
| Basic
Aerodynamics |
Communication Procedures |
Enroute Flight |
|
Flight Instruments
|
Navigation |
Procedures and Airport Operations |
| Regulations | Weather | Weather Services | First Aid & Physiology |
Aircraft & Human Performance
Table of Contents
Weight and BalanceAirplane
CG Shift With FuelBurn
Weight-Shift Control
Powered Parachute
Computing Weight and Balance Problems Using a Table
Computing Weight and Balance Problems Using a Graph
Density Altitude and Aircraft Performance
Takeoff Distance
Cruise Power Setting Table
Landing Distance Graphs and Tables
Headwind and Crosswind Component Graph
Human Performance & Risk Management
Risk Mitigation
Weight and Balance
Even though an aircraft has been certificated for flight at a specified maximum gross weight, it may not be safe to take off with that load under all conditions. High altitude, high temperature, and high humidity are additional factors which may require limiting the load to some weight less than the maximum allowable.
Some of the problems caused by overloading an aircraft are:
• The aircraft will need a higher takeoff speed, which results in a longer takeoff run.
• Both the rate and angle of climb will be reduced.
• The service ceiling will be lowered.
• The cruising speed will be reduced.
• The cruising range will be shortened.
• Maneuverability will be decreased.
• A longer landing roll will be required because the landing speed will be higher.
• Excessive loads will be imposed on the structure, especially the landing gear.
The empty weight is obtained from appropriate charts. It includes the airframe, engine, all fixed equipment, and unusable fuel and oil. Some aircraft include all oil in the aircraft empty weight. The useful load includes the pilot, passengers, baggage, fuel and oil. The takeoff weight is the empty weight plus the useful load. The landing weight is the takeoff weight minus any fuel used.
The arm is the horizontal distance measured in inches from the datum line to a point on the aircraft. If measured aft, toward the tail, the arm is given a positive (+) value; if measured forward, toward the nose, the arm is given a negative (-) value. See Figure 8-1.
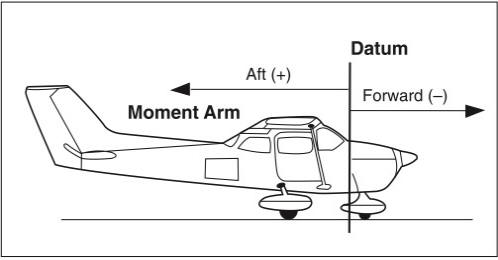
The moment is the product of the weight of an object multiplied by its arm and is expressed in pound-inches (lbs-in). A formula that is used to find moment is usually expressed as follows:
Weight × Arm = Moment
The moment index is a moment divided by a constant such as 100 or 1,000. It is used to simplify computations where heavy items and long arms result in large, unmanageable numbers. This is usually expressed as MOM/100 or MOM/1000, etc.
The center of gravity (CG) is the point about which an aircraft will balance, and it is expressed in inches from datum. The center of gravity is found by dividing the total moment by the total weight, and the formula is usually expressed as follows:
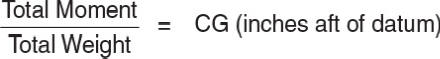
Standard weights have been established for numerous items involved in weight and balance computations. These weights should not be used if actual weights are available. Some of the standard weights are:
Airplane
In addition to considering the weight to be carried, the pilot must ensure that the load is arranged to keep the aircraft in balance. The balance point, or CG, is the point at which all of the weight of the airplane is considered to be concentrated. For an aircraft to be safe to fly, the center of gravity must fall between specified limits. All aircraft categories have unique balance requirements; some need to be balanced precisely while others are less sensitive to fore and aft weight distribution. The specific balance requirements for each aircraft category are covered in the POH and will be tested on during the practical (checkride). To keep the CG within safe limits it may be necessary to move weight toward the nose of the aircraft (forward), which moves the CG forward, or toward the tail (aft) which moves the CG aft.
The specified forward and aft points within which the CG must be located for safe flight are called the center of gravity limits. These limits are specified by the manufacturer. The distance between the forward and aft CG limits is called the center of gravity range.
CG Shift With Fuel Burn
When Fuel is burned, the CG shifts, depending on the Fuel Tank Configuration
in the wing. In Swept wing aircraft, fuel burn shifts the CG forward. In a
Cessna 182, Fuel Burn causes the shift forward. See the below W/B report from
Fltplan.com:
Weight-Shift Control
Weight and loading is typically used for weight-shift control. The cart normally does not have balance requirements, but the attachment point to the cart is specified in the POH.
Powered Parachute
Weight and loading is used for powered parachutes. The POH procedure for the fore and aft attachment points of the wing to the cart must be followed so that the cart will obtain the proper deck angle (the angle of the cart bottom with the horizontal plane).
Computing Weight and Balance Problems Using a Table
Problem:
Determine if the airplane weight and balance is within limits.
Solution:
1. Determine the total weight. Using the information provided in the question, enter the items and the weights:
| Item | Weight | (lbs) | Arm | (in) | Moment | (lbs-in) |
|---|---|---|---|---|---|---|
| Front seat occupants | 340 | |||||
| Rear seat occupants | 295 | |||||
| Fuel (main wing tanks) | 264 | * | ||||
| Baggage | 56 | |||||
| Empty weight | + 2,015 | ** | ||||
| 2,970 | lbs | |||||
| *44 gal × 6 lbs/gal **found in FAA Figure 33 | ||||||
2. Fill in the arms (found in FAA Figure 32) and calculate the moments. Moments are determined by multiplying in each row: weight × arm. Then divide that moment by 100 to keep the number a manageable size, and finally, total all moments.
| Item | Weight | (lbs) | Arm | (in) | Moment/100 | (lbs-in) |
|---|---|---|---|---|---|---|
| Front seat occupants | 340 | 85 | 289.0 | |||
| Rear seat occupants | 295 | 121 | 357.0 | |||
| Fuel (main wing tanks) | 264 | 75 | 198.0 | |||
| Baggage | 56 | 140 | 78.4 | |||
| Empty weight | + 2,015 | 1,554.0 | ||||
| 2,970 | lbs | 2,476.4 | lbs-in |
3. Determine the balance conditions. Looking at FAA Figure 33, notice that the table stops at the maximum weight of 2,950. Even though the weight is off the scale, the Moment of 2,476.4 is between the minimum and maximum Moment limits given in the table. Therefore, we are 20 pounds overweight and within balance limits.
Computing Weight and Balance Problems Using a Graph
Problem:
Referring to FAA Figure 34, determine the maximum amount of baggage that may be loaded aboard the airplane for the CG to remain within the loading envelope.
| Item | Weight | (lbs) | Moment/1,000 | (lbs-in) |
|---|---|---|---|---|
| Empty weight | 1,350 | 51.5 | ||
| Pilot, front passenger | 250 | — | ||
| Rear passengers | 400 | — | ||
| Baggage | — | — | ||
| Fuel 30 gal. | — | — | ||
| Oil 8 qt. | — | — |
Solution:
1. Determine the total weight. Using the information provided in the question, enter the items and the weights:
| Item | Weight | (lbs) | Moment/1,000 | (lbs-in) |
|---|---|---|---|---|
| Pilot, front passenger | 250 | |||
| Rear passengers | 400 | |||
| Fuel | 180 | * | ||
| Oil | 15 | ** | ||
| Baggage | — | |||
| Empty weight | + 1,350 | † | ||
| 2,195 | lbs | |||
| *30 gal × 6 lbs/gal **given in the note in the middle of FAA Figure 34 † given in problem | ||||
2. Determine the moments. Using FAA Figure 34, locate the moments for all the given weights:
| Item | Weight | (lbs) | Moment/1,000 | (lbs-in) |
|---|---|---|---|---|
| Pilot, front passenger | 250 | 9.3 | ||
| Rear passengers | 400 | 29.3 | ||
| Fuel | 180 | 8.7 | ||
| Oil | 15 | -0.2 | * | |
| Baggage | — | — | ||
| Empty weight | + 1,350 | 51.5 | ||
| 2,195 | lbs | 98.6 | lbs-in | |
| *from note in center of FAA Figure 34 | ||||
3. From the Center of Gravity Moment Envelope, at the bottom of FAA Figure 34, determine the maximum allowable gross weight of the aircraft, as indicated by the top of the “Normal Category” envelope (2,300 pounds). Comparing the total weight of this problem with the maximum allowable weight shows that 105 pounds of baggage could be carried:
| 2,300 |
| – 2,195 |
| 105 |
4. From the Loading Graph, determine the MOM/1000 of 105 pounds of baggage.
Add that amount to the previous total MOM/1000:
| Item | Weight | (lbs) | Moment/1,000 | (lbs-in) |
|---|---|---|---|---|
| Totals | 2,195 | 98.6 | ||
| Baggage | + 105 | + 10.0 | ||
| New Totals | 2,300 | lbs | 108.6 | lbs-in |
5. Enter the Center of Gravity Moment Envelope Graph at the total Mom/1,000 (108.6) and the maximum allowable gross weight line at 2,300 pounds. The point of intersection falls within the “Normal Category” envelope and acceptable weight and balance conditions.
Video Examples for Weight and Balance Problems 3:43
https://tomgorski.com/video/Weight_Balance_Examples.mp4
Density Altitude and Aircraft Performance
Aircraft performance charts show a pilot what can be expected of an airplane (rate of climb, takeoff roll, etc.) under stipulated conditions. Prediction of performance is based upon a sea level temperature of +15°C (+59°F) and atmospheric pressure of 29.92 "Hg (1013.2 mb). This combination of temperature and pressure is called a standard day. When the air is at a standard density, temperature and/or pressure deviations from standard will change the air density or the density altitude, which affects aircraft performance. Performance charts allow the pilot to predict how an aircraft will perform.
Relative humidity also affects density altitude, but is not considered when the performance charts are formulated. A combination of high temperature, high humidity, and high altitude result in a density altitude higher than the pressure altitude which, in turn, results in reduced aircraft performance.
Problem:
Using the Density Altitude Chart shown in FAA Figure 8, and the following conditions, determine the density altitude.
Conditions:
Solution:
1. Determine the applicable altitude correction for the altimeter setting of 30.35 "Hg. See FAA Figure 8. That setting is not shown on the chart, so it is necessary to interpolate between the correction factors shown for 30.30 "Hg and 30.40 "Hg. To interpolate, add the two factors and divide by 2:
-348 + (-440) = -788
-788 ÷ 2 = -394
Since the result is a negative number, subtract that value from the given airport elevation:
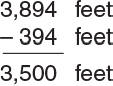
2. Along the bottom of the chart, locate the given OAT (+25°F). From that point, proceed upward until intersecting the pressure altitude line that is equal to the corrected airport elevation (3,500 feet). From that point, proceed to the left and read the density altitude (2,000 feet).
Note that high-density altitude reduces propeller efficiency as well as overall aircraft performance.
Takeoff Distance
The Takeoff Distance Graph, FAA Figure 40, allows the pilot to determine the ground roll required for takeoff under various conditions. It also shows the total distance required for a takeoff and climb to clear a 50-foot obstacle.
Problem:
Using the Takeoff Distance Graph shown in FAA Figure 40, determine the approximate ground roll distance for takeoff and the total distance for a takeoff to clear a 50-foot obstacle under the following conditions:
Solution:
1. Locate the OAT, 90°F, on the graph.
2. From that point, draw a line upward to the line representing the pressure altitude of 2,000 feet.
3. From the point of intersection, draw a line to the right to the reference line.
4. From that point, proceed downward and to the right (remaining proportionally between the existing guide lines) to the vertical line representing 2,500 pounds.
5. From there, draw a line to the right to the second reference line.
6. Then proceed down and to the right (remaining proportionally between the existing guide lines) to the line representing the 20-knot headwind component line.
7. From there, draw a line to the right to the third reference line.
8. From here, move to the right and read approximate ground roll for takeoff of 650 feet.
9. Proceed upward and to the right (remaining proportionately between the existing guide lines) to the vertical line representing a 50-foot obstacle and read the approximate total distance to clear a 50-foot obstacle (1,100 feet).
Cruise Power Setting Table
The Cruise Power Setting Table (FAA Figure 35) may be used to forecast fuel flow and true airspeed and, therefore allow a pilot to determine the amount of fuel required and the estimated time en route.
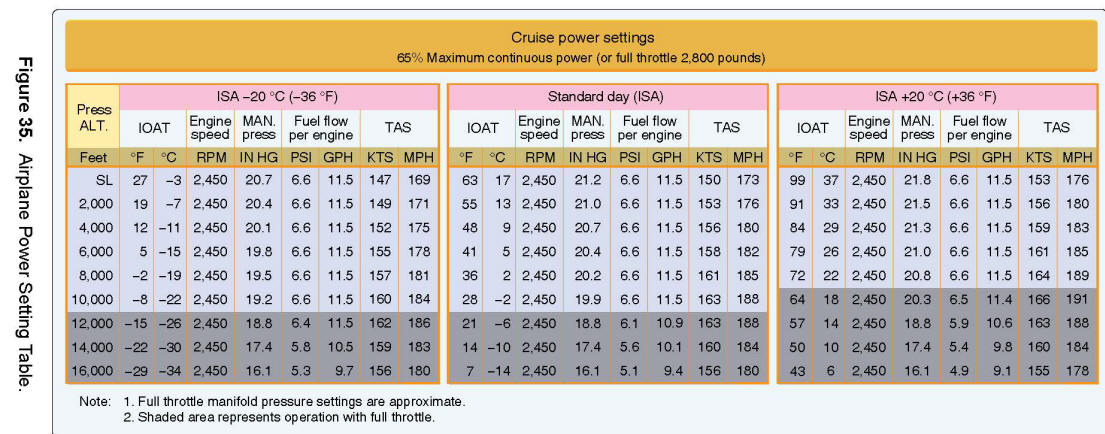
Problem:
Using the Cruise Power Setting Table shown in FAA Figure 35, determine the expected fuel consumption for a 1,000-statute-mile flight under the following conditions:
Solution:
1. Find the fuel flow and TAS. Enter the chart at the 8,000-foot pressure altitude line and proceed to the right and identify the chart which represents an indicated outside air temperature (IOAT) of -19°C at 8,000 feet (the chart for ISA -20°C). Continue reading to the right, noting the manifold pressure of 19.5 "Hg, the fuel flow per engine will be 6.6 pounds per square inch or 11.5 gallons per hour (GPH), and the TAS will be 157 knots or 181 mph.
2. Calculate the time flown. Using a flight computer, calculate the time en route:
1,000 SM at 181 mph = 5.52 hours
3. Calculate the fuel consumption. Using a flight computer, calculate the fuel burned in this time:
5.52 hours × 11.5 GPH = 63.48 gallons consumed
Landing Distance Graphs and Tables
Some landing distance graphs such as the one shown in FAA Figure 37, are used in the same manner as the takeoff distance graph.
Another type of landing distance table is shown in FAA Figure 38.
Problem:
Using the Landing Distance Table shown in FAA Figure 38, determine the total distance required to land over a 50-foot obstacle.
Solution:
Enter FAA Figure 38 at 5,000 feet and 41°F to find 1,195 feet is required to clear a 50-foot obstacle. Note #1 states an additional correction is necessary for the headwind, 10 percent for each 4 knots. This would mean 20 percent for 8 knots. 20 percent of 1,195 feet is 239 feet, resulting in 956 feet—total distance required to land:
1,195 × .20 = 239 feet
1,195 – 239 = 956 feet
Headwind and Crosswind Component Graph
In general, taking off into a wind improves aircraft performance, and reduces the length of runway required to become airborne. The stronger the wind, the better the aircraft performs. Crosswinds, however, may make the aircraft difficult or impossible to control. The aircraft manufacturer determines the safe limit for taking off or landing with a crosswind and establishes the maximum allowable crosswind component. The graph shown in FAA Figure 36 is used to determine what extent a wind of a given direction and speed is felt as a headwind and/or crosswind.
Problem:
The wind is reported to be from 085° at 30 knots, and you plan to land on Runway 11. What will the headwind and crosswind components be?
Solution:
1. Determine the angular difference between the wind direction and the runway:

2. Find the intersection of the 25°-angle radial line and the 30-knot wind speed arc on the graph shown in FAA Figure 36. From the intersection move straight down to the bottom of the chart and read that the crosswind component equals 13 knots. From the point of intersection move horizontally left and read that the headwind component equals 27 knots.
Human Performance & Risk Management
From the FAA Risk Management Handbook:
https://www.faa.gov/regulations_policies/handbooks_manuals/aviation
Hazardous attitudes occur to every pilot to some degree at some time.
What are some of these hazardous attitudes?
Antiauthority, impulsivity, macho, resignation, and invulnerability.
Risk management, as part of the aeronautical decision making (ADM)
process, relies on which features to reduce the risks associated with each
flight?
Situational awareness, problem recognition, and good judgment.
What is the Risk Management process?
Risk management is a three-step process to:
1- Identify hazards,
2- Assess how likely those hazards are to negatively impact their operations,
and,
3- Reduce the chances that those hazards will cause an accident.
A predisposition to respond to persons, situations, or events in a given
manner reveals a person’s attitude. Studies have identified
five hazardous attitudes that can affect a pilot’s ability to make sound
decisions and exercise authority properly. [Figure 3-1]
Most pilots sincerely believe that they will respond to hazards
appropriately and take actions necessary to avoid accidents.
However, a pilot’s attitude affects perception of hazards, the analysis of the
potential threat, and performance of an appropriate
response.
A pilot with approximately 233 hours of total time rented an unfamiliar airplane
for a round-trip VFR cross-country flight. The
pilot had about 2.6 hours of time in the specific make and model. The NTSB
narrative indicates the following:
According to the operator of the airplane, the pilot had difficulty starting
the engine prior to departing for Erie
International/Tom Ridge Field (KERI), and requested assistance. The operator
proceeded out to the airplane, and
showed the pilot how to start the engine. The operator then suggested the pilot
leave Erie with enough time to return to
Waterbury-Oxford Airport (KOXC) before sunset. Later in the day, the pilot
called the operator and informed him that
the airplane operated fine on the flight to Erie, and he would be back at
Waterbury-Oxford by 19:00.
The pilot actually departed Erie at night. There was a fatal crash and the NTSB
probable cause states:
The loss of partial engine power for undetermined reasons, and the pilot’s
loss of control after performing an evasive
maneuver to avoid trees during a forced landing at night. Factors related to the
accident were a rough running engine
and the pilots inability to see the trees due to the nighttime conditions. The
NTSB accident details are available here.
While not common, even professionally trained pilots sometimes fail to recognize
and respond to hazards and associated risks.
An airline accident involving a transport category turbojet taken to its maximum
operating altitude resulted in both engines
flaming out after an aerodynamic stall. The flight ended in a crash and two
fatalities. The NTSB probable cause(s) follows:
The National Transportation Safety Board determines the probable cause(s) of
this accident to be: (1) the pilots’
unprofessional behavior, deviation from standard operating procedures, and poor
airmanship, which resulted in an
in-flight emergency from which they were unable to recover, in part because of
the pilots’ inadequate training; (2)
the pilots’ failure to prepare for an emergency landing in a timely manner,
including communicating with air traffic
controllers immediately after the emergency about the loss of both engines and
the availability of landing sites; and
(3)the pilots’ improper management of the double engine failure checklist, which
allowed the engine cores to stop rotating
and resulted in the core lock engine condition. Contributing to this accident
were (1) the core lock engine condition,
which prevented at least one engine from being restarted, and (2) the airplane
flight manuals that did not communicate
to pilots the importance of maintaining a minimum airspeed to keep the engine
cores rotating. The NTSB accident
details are available at the NTSB website. https://www.ntsb.gov
Since attitude influences behavior, pilots should consider their own
attitude and the antidote to any hazardous attitude. [Figure
3-2 Below] The pilots in the two fatal accidents described above exhibited several of
these hazardous attitudes. If they had recognized
their attitude toward the hazards and associated risks and considered that their
behavior could result in an accident, it is very
likely that they would have acted differently (invulnerability). If the general
aviation pilot had waited and returned the next
day, he might be alive today (impulsivity). The commercial pilots wanted to
claim they had flown the aircraft at its maximum
altitude (macho). Pilot attitudes regarding hazard analysis clearly play a role
in decision-making.
Risk Mitigation
The words “hazard” and “risk” seem simple, but these words are easily
confused.
14 CFR part 5, section 5.5 defines these two terms as follows:
• Hazard – a condition that could foreseeably cause or contribute to an aircraft
accident as defined in 49 CFR part 830,
section 830.2.
• Risk – the composite of predicted severity and likelihood of the potential
effect of a hazard.
14611
Simply put, a hazard is a condition that could cause an accident. The
probability and predicted severity of the consequences
that may result from any hazard is the risk. Identifying, analyzing, and
responding appropriately to hazards decreases the risks
and increases the margin of safety.
Risk mitigation identifies hazards and reduces the likelihood or
potential severity of associated risks. It may allow a pilot to
undertake a flight that would otherwise generate unacceptable risk. In other
cases, the risk mitigation process may identify high
and serious risks that cannot be mitigated, which may require rescheduling,
cancellation, or alternate transportation.
A brief FAA Safety Team (FAASTeam) video on risk-based decision-making summarizes many concepts.